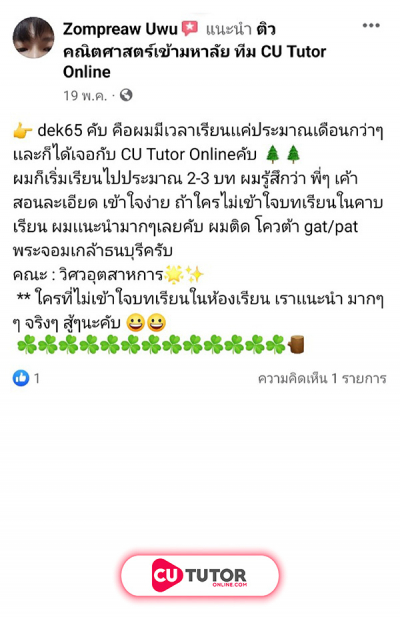
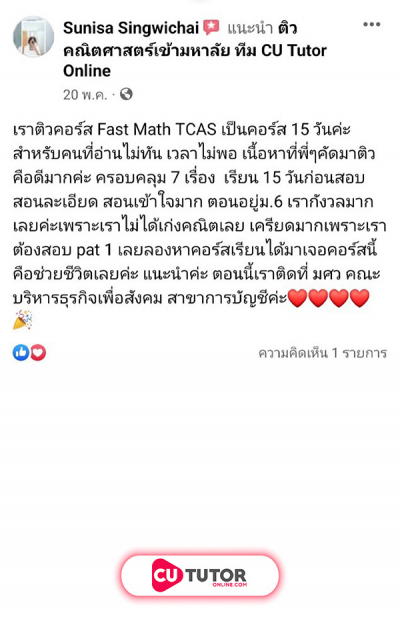
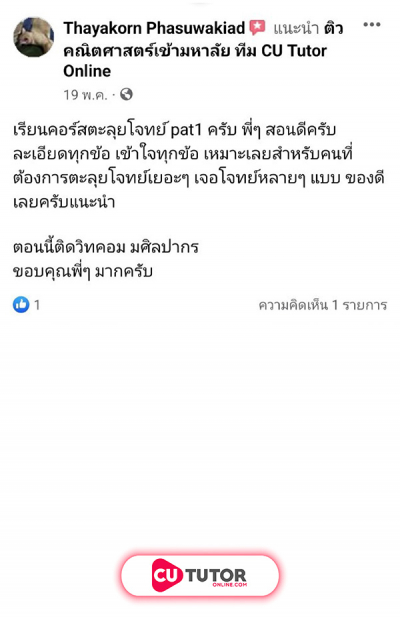
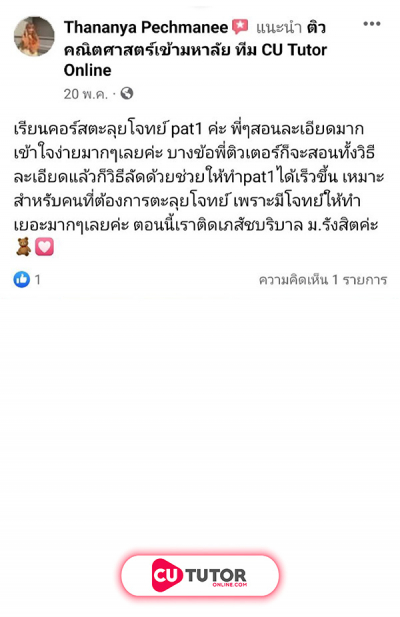
กล่องใบหนึ่งบรรจุลูกแก้วสีแดง 2 ลูก ลูกแก้วสีขาว 3 ลูก และลูกแก้วสีเขียว 3 ลูก สุ่มหยิบลูกแก้วออกมาจากกล่อง 8 ครั้ง ครั้งละลูกโดยไม่ต้องใส่คืน ความน่าจะเป็นที่สุ่มหยิบลูกแก้ว 8 ครั้ง โดยครั้งที่ 1 ได้ลูกแก้วสีขาวหรือหยิบครั้งที่ 8 ไม่ได้ลูกแก้วสีแดง เท่ากับข้อใดต่อไปนี้