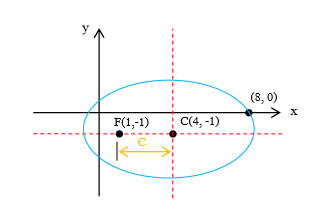
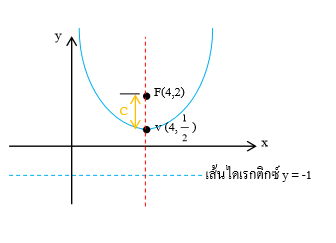
กำหนดให้วงรีรูปหนึ่ง ผ่านจุด มีจุดศูนย์กลางอยู่ที่ และโฟกัสจุดหนึ่งอยู่ที่ ถ้าพาราโบลารูปหนึ่งมีโฟกัสอยู่ที่จุดปลายของแกนโทของวงรีในควอดรันต์ (quardrant) ที่ 1 และมีเส้นไดเรกตริกซ์ทับกับแกนเอกของวงรี แล้วสมการของพาราโบลารูปนี้ตรงกับสมการในข้อใดต่อไปนี้