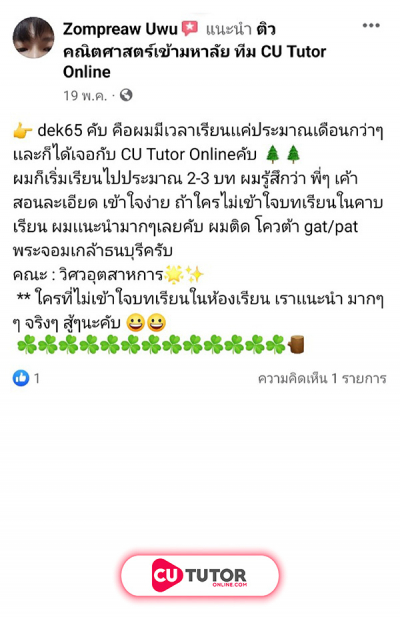
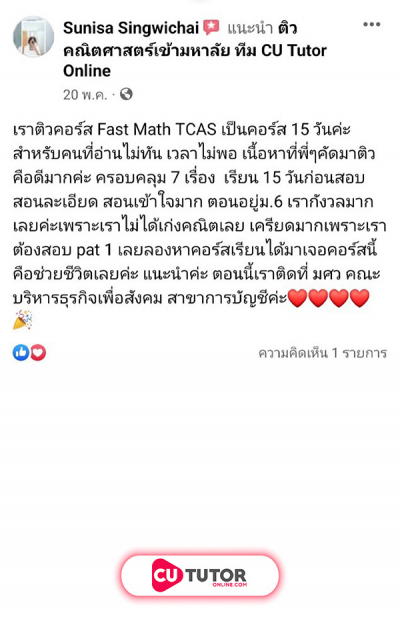
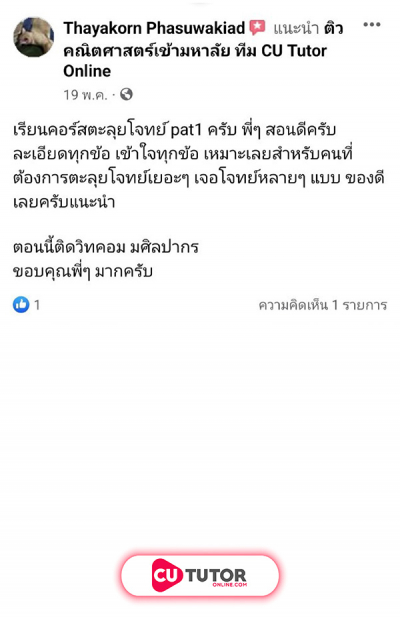
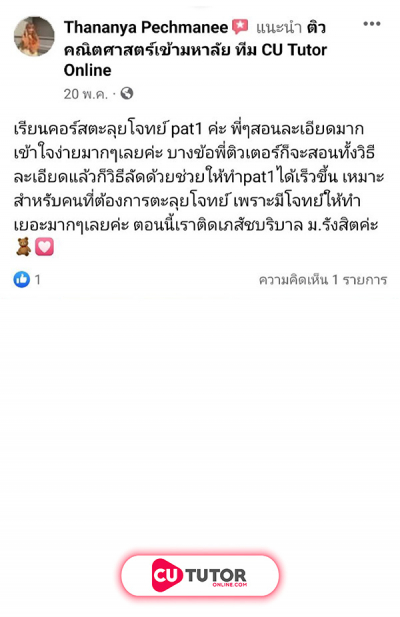
ด.ญ.ปาหนัน ได้รางวัลจากการแข่งขันตอบปัญหาทางคณิตศาสตร์เป็นเงิน บาท
เธอตั้งใจจะออมเงินและนำเงินมารวมกับเงินรางวัลที่ได้ เพื่อซื้อหนังซื้อนวนิยายชุดหนึ่ง ราคา บาท
ถ้าในวันแรก ด.ญ.ปาหนัน ออมเงินไว้ บาท และในวันต่อๆ มาจะออมเพิ่มจากวันก่อนหน้าวันละ บาท ทุกๆ วัน
แล้วจำนวนวันที่น้อยที่สุดที่ ด.ญ.ปาหนัน ต้องออมเงินเพื่อให้พอซื้อหนังสือชุดดังกล่าว เท่ากับข้อใดต่อไปนี้


.PNG)