ให้ A เป็นเซตคำตอบของสมการ และให้ B เป็นเซตคำตอบของสมการ จำนวนสมาชิกของเซต เท่ากับเท่าใด เมื่อ แทนเพาเวอร์เซตของเซต
เฉลยข้อสอบ
.png)
ทำให้ sinA =
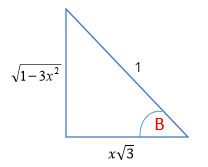
ทำให้ sinB =
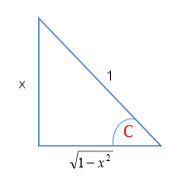
ทำให้ sinC = x
ให้ A เป็นเซตคำตอบของสมการ และให้ B เป็นเซตคำตอบของสมการ จำนวนสมาชิกของเซต เท่ากับเท่าใด เมื่อ แทนเพาเวอร์เซตของเซต
.png)
ทำให้ sinA =

ทำให้ sinB =

ทำให้ sinC = x